A Machine Is a Device That Can Multiply _________________

Mechanical machine for arithmetic operations for absolute calculators

Various desktop mechanical calculators used in the part from 1851 onwards. Each one has a different user interface. This moving picture shows clockwise from meridian left: An Arithmometer, a Comptometer, a Dalton adding machine, a Sundstrand, and an Odhner Arithmometer

A mechanical calculator, or calculating machine, is a mechanical device used to perform the basic operations of arithmetic automatically, or (historically) a simulation such equally an analog computer or a slide rule. About mechanical calculators were comparable in size to pocket-size desktop computers and have been rendered obsolete by the advent of the electronic computer and the digital computer.

Surviving notes from Wilhelm Schickard in 1623 reveal that he designed and had built the primeval of the modern attempts at mechanizing calculation. His auto was composed of two sets of technologies: first an abacus made of Napier'due south bones, to simplify multiplications and divisions offset described six years earlier in 1617, and for the mechanical office, it had a dialed pedometer to perform additions and subtractions. A study of the surviving notes shows a car that would have jammed after a few entries on the same punch,^[one] and that information technology could be damaged if a deport had to be propagated over a few digits (similar adding 1 to 999).^[2] Schickard abased his project in 1624 and never mentioned information technology once again until his decease xi years subsequently in 1635.

Two decades later Schickard's supposedly failed try, in 1642, Blaise Pascal decisively solved these particular bug with his invention of the mechanical calculator.^[iii] Co-opted into his father'south labour as taxation collector in Rouen, Pascal designed the calculator to help in the big amount of dull arithmetic required;^[4] it was called Pascal's Calculator or Pascaline.^[5]

Thomas' arithmometer, the first commercially successful automobile, was manufactured 2 hundred years after in 1851; information technology was the offset mechanical calculator strong enough and reliable enough to be used daily in an office environment. For forty years the arithmometer was the merely blazon of mechanical computer available for sale.^[6]

The comptometer, introduced in 1887, was the kickoff machine to use a keyboard that consisted of columns of nine keys (from 1 to 9) for each digit. The Dalton calculation machine, manufactured in 1902, was the first to have a ten key keyboard.^[vii] Electric motors were used on some mechanical calculators from 1901.^[viii] In 1961, a comptometer type motorcar, the Anita mk7 from Sumlock comptometer Ltd., became the first desktop mechanical calculator to receive an all-electronic calculator engine, creating the link in between these ii industries and marking the beginning of its pass up. The product of mechanical calculators came to a end in the eye of the 1970s closing an industry that had lasted for 120 years.

Charles Babbage designed two new kinds of mechanical calculators, which were so big that they required the ability of a steam engine to operate, and that were too sophisticated to be built in his lifetime. The get-go one was an automatic mechanical calculator, his difference engine, which could automatically compute and print mathematical tables. In 1855, Georg Scheutz became the first of a handful of designers to succeed at building a smaller and simpler model of his departure engine.^[9] The second ane was a programmable mechanical reckoner, his analytical engine, which Babbage started to design in 1834; "in less than two years he had sketched out many of the salient features of the modern computer. A crucial stride was the adoption of a punched card system derived from the Jacquard loom"^[ten] making it infinitely programmable.^[11] In 1937, Howard Aiken convinced IBM to blueprint and build the ASCC/Mark I, the first auto of its kind, based on the architecture of the analytical engine;^[12] when the machine was finished some hailed it as "Babbage'southward dream come true".^[13]

Ancient history [edit]

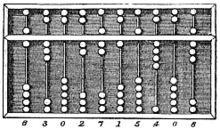
A Chinese Suanpan (the number represented in the picture is vi,302,715,408)

The want to economize time and mental effort in arithmetical computations, and to eliminate homo liability to error, is probably as onetime every bit the scientific discipline of arithmetic itself. This desire has led to the pattern and construction of a multifariousness of aids to calculation, commencement with groups of small objects, such equally pebbles, first used loosely, later every bit counters on ruled boards, and later yet equally beads mounted on wires stock-still in a frame, every bit in the abacus. This instrument was probably invented past the Semitic races and later adopted in India, whence it spread west throughout Europe and e to China and Japan.
After the development of the abacus, no further advances were fabricated until John Napier devised his numbering rods, or Napier's Bones, in 1617. Various forms of the Bones appeared, some budgeted the offset of mechanical computation, simply it was not until 1642 that Blaise Pascal gave us the first mechanical computing machine in the sense that the term is used today.

—Howard Aiken, Proposed automated calculating machine, presented to IBM in 1937

A short listing of other precursors to the mechanical computer must include a group of mechanical analog computers which, once set, are only modified by the continuous and repeated action of their actuators (creepo handle, weight, wheel, water...). Before the mutual era, there are odometers and the Antikythera machinery, a seemingly out of place, unique, geared astronomical clock, followed more than than a millennium later by early mechanical clocks, geared astrolabes and followed in the 15th century by pedometers. These machines were all made of toothed gears linked past some sort of deport mechanisms. These machines always produce identical results for identical initial settings different a mechanical calculator where all the wheels are contained simply are also linked together by the rules of arithmetic.

The 17th century [edit]

Overview [edit]

The 17th century marked the beginning of the history of mechanical calculators, as it saw the invention of its beginning machines, including Pascal's estimator, in 1642.^{[4] [14]} Blaise Pascal had invented a machine which he presented as beingness able to perform computations that were previously idea to be merely humanly possible.^[15]

In a sense, Pascal's invention was premature, in that the mechanical arts in his time were not sufficiently advanced to enable his machine to be fabricated at an economic toll, with the accuracy and strength needed for reasonably long use. This difficulty was not overcome until well on into the nineteenth century, by which time as well a renewed stimulus to invention was given by the demand for many kinds of adding more intricate than those considered by Pascal.

—S. Chapman, Pascal tercentenary celebration, London, (1942)^[16]

The 17th century also saw the invention of some very powerful tools to assist arithmetics calculations like Napier'southward bones, logarithmic tables and the slide dominion which, for their ease of use by scientists in multiplying and dividing, ruled over and impeded the use and evolution of mechanical calculators^[17] until the production release of the arithmometer in the mid 19th century.

Invention of the mechanical calculator [edit]

Blaise Pascal invented a mechanical calculator with a sophisticated comport mechanism in 1642. After iii years of effort and l prototypes^[19] he introduced his figurer to the public. He built twenty of these machines in the following ten years.^[xx] This machine could add and decrease two numbers directly and multiply and split up by repetition. Since, unlike Schickard'southward machine, the Pascaline dials could only rotate in 1 direction zeroing it after each calculation required the operator to dial in all 9s and then (method of re-zeroing) propagate a carry right through the machine.^[21] This suggests that the conduct mechanism would have proved itself in practice many times over. This is a attestation to the quality of the Pascaline because none of the 17th and 18th century criticisms of the machine mentioned a problem with the conduct mechanism and yet it was fully tested on all the machines, by their resets, all the time.^[22]

Pascal's invention of the calculating car, just iii hundred years ago, was made while he was a youth of 19. He was spurred to it past seeing the brunt of arithmetical labour involved in his begetter'due south official work as supervisor of taxes at Rouen. He conceived the idea of doing the piece of work mechanically, and developed a blueprint appropriate for this purpose; showing herein the same combination of pure scientific discipline and mechanical genius that characterized his whole life. But it was ane matter to excogitate and design the motorcar, and another to become it made and put into use. Here were needed those applied gifts that he displayed subsequently in his inventions...

—South. Chapman, Pascal tercentenary celebration, London, (1942)^[xvi]

In 1672, Gottfried Leibniz started working on calculation direct multiplication to what he understood was the working of Pascal's calculator. However, it is doubtful that he had ever fully seen the mechanism and the method could non have worked because of the lack of reversible rotation in the mechanism. Accordingly, he eventually designed an entirely new machine chosen the Stepped Reckoner; it used his Leibniz wheels, was the first two-motion calculator, the first to use cursors (creating a memory of the commencement operand) and the outset to have a movable carriage. Leibniz built two Stepped Reckoners, one in 1694 and ane in 1706.^[23] Only the motorcar built in 1694 is known to exist; it was rediscovered at the cease of the 19th century having been forgotten in an cranium in the University of Göttingen.^[23]

In 1893, the German calculating machine inventor Arthur Burkhardt was asked to put Leibniz machine in operating condition if possible. His written report was favorable except for the sequence in the carry.^[24]

Leibniz had invented his namesake cycle and the principle of a 2-move calculator, but later forty years of development he wasn't able to produce a automobile that was fully operational;^[25] this makes Pascal's calculator the only working mechanical calculator in the 17th century. Leibniz was also the showtime person to draw a pinwheel figurer.^[26] He once said "It is unworthy of excellent men to lose hours like slaves in the labour of calculation which could safely be relegated to anyone else if machines were used."^[27]

Other calculating machines [edit]

Schickard, Pascal and Leibniz were inevitably inspired by the role of clockwork which was highly historic in the seventeenth century.^[28] However, uncomplicated-minded application of interlinked gears was insufficient for any of their purposes. Schickard introduced the utilize of a single toothed "mutilated gear" to enable the carry to accept place. Pascal improved on that with his famous weighted sautoir. Leibniz went even further in relation to the power to use a moveable carriage to perform multiplication more than efficiently, albeit at the expense of a fully working carry machinery.

...I devised a tertiary which works past springs and which has a very uncomplicated design. This is the one, as I have already stated, that I used many times, hidden in the manifestly sight of an infinity of persons and which is yet in operating social club. Yet, while always improving on it, I found reasons to modify its pattern...

—Pascal, Ad Necessary to those who have curiosity to see the Arithmetic Machine, and to operate it (1645)^[29]

When, several years ago, I saw for the offset fourth dimension an instrument which, when carried, automatically records the numbers of steps by a pedestrian, information technology occurred to me at in one case that the entire arithmetic could exist subjected to a similar kind of machinery so that not only counting only also improver and subtraction, multiplication and division could exist accomplished by a suitably arranged machine easily, promptly, and with certain results

—Leibniz, on his calculating machine (1685)^[30]

The principle of the clock (input wheels and display wheels added to a clock similar machinery) for a direct-entry calculating car couldn't be implemented to create a fully effective calculating motorcar without boosted innovation with the technological capabilities of the 17th century.^[31] considering their gears would jam when a carry had to be moved several places along the accumulator. The only 17th-century calculating clocks that have survived to this day do not have a automobile-broad comport mechanism and therefore cannot be called fully constructive mechanical calculators. A much more than successful calculating clock was congenital by the Italian Giovanni Poleni in the 18th century and was a two-movement calculating clock (the numbers are inscribed first and then they are processed).

• In 1623, Wilhelm Schickard, a German professor of Hebrew and Astronomy, designed a calculating clock which he drew on 2 letters that he wrote to Johannes Kepler. The starting time auto to be built by a professional was destroyed during its construction and Schickard abandoned his projection in 1624. These drawings had appeared in various publications over the centuries, starting in 1718 with a volume of Kepler'due south messages by Michael Hansch,^[32] merely in 1957 it was presented for the get-go fourth dimension as a long-lost mechanical estimator by Dr. Franz Hammer. The building of the first replica in the 1960s showed that Schickard's machine had an unfinished design and therefore wheels and springs were added to make information technology work.^[33] The use of these replicas showed that the single-tooth wheel, when used within a calculating clock, was an inadequate carry mechanism.^[34] (see Pascal versus Schickard). This did not mean that such a machine could not be used in practice, simply the operator when faced with the machinery resisting rotation, in the unusual circumstances of a carry being required beyond (say) 3 dials, would need to "help" the subsequent carry to propagate.
• Around 1643, a French clockmaker from Rouen, later hearing of Pascal'due south piece of work, congenital what he claimed to be a computing clock of his own design. Pascal fired all his employees and stopped developing his estimator as before long every bit he heard of the news.^[35] It is only after being assured that his invention would be protected by a royal privilege that he restarted his activity.^[36] A careful test of this calculating clock showed that it didn't work properly and Pascal called it an avorton (aborted fetus).^{[37] [38]}
• In 1659, the Italian Tito Livio Burattini built a machine with 9 contained wheels, each one of these wheels was paired with a smaller carry wheel.^[39] At the end of an operation the user had to either manually add each carry to the side by side digit or mentally add these numbers to create the last result.
• In 1666, Samuel Morland invented a auto designed to add sums of coin,^[40] merely it was not a true calculation machine since the acquit was added to a small carry cycle situated above each digit and not directly to the next digit. It was very similar to Burattini's machine. Morland created besides a multiplying machines with interchangeable disks based on Napier'south bones.^{[41] [42]} Taken together these two machines provided a capacity similar to that of the invention of Schickard, although information technology is doubtful that Morland ever encountered Schickard's calculating clock.
• In 1673, the French clockmaker René Grillet described in Curiositez mathématiques de 50'invention du Sr Grillet, horlogeur à Paris a calculating machine that would be more compact than Pascal's computer and reversible for subtraction. The simply two Grillet machines known^[43] have no acquit mechanism, displaying iii lines of nine contained dials they besides have nine rotating napier's rod for multiplication and sectionalization. Contrary to Grillet's merits, it was not a mechanical calculator after all.^[44]

The 18th century [edit]

Detail of a replica of an 18th-century calculating machine, designed and built in by the German Johann Helfrich Müller.

Overview [edit]

The 18th century saw the kickoff mechanical calculator that could perform a multiplication automatically; designed and built by Giovanni Poleni in 1709 and fabricated of woods, it was the first successful calculating clock. For all the machines built in this century, division still required the operator to decide when to cease a repeated subtraction at each index, and therefore these machines were just providing a help in dividing, like an abacus. Both pinwheel calculators and Leibniz cycle calculators were built with a few unsuccessful attempts at their commercialization.

Prototypes and limited runs [edit]

• In 1709, the Italian Giovanni Poleni was the first to build a calculator that could multiply automatically. It used a pinwheel design, was the start operational calculating clock and was fabricated of wood;^[45] he destroyed it after hearing that Antonius Braun had received 10,000 Guldens for dedicating a pinwheel machine of his own blueprint to the emperor Charles VI of Vienna.^[46]
• In 1725, the French University of Sciences certified a calculating auto derived from Pascal's calculator designed by Lépine, a French craftsman. The automobile was a bridge in betwixt Pascal's estimator and a calculating clock. The carry transmissions were performed simultaneously, like in a calculating clock, and therefore "the machine must have jammed beyond a few simultaneous carry transmissions".^[47]
• In 1727, a German, Antonius Braun, presented the beginning fully functional 4-operation machine to Charles VI, Holy Roman Emperor in Vienna. Information technology was cylindrical in shape and was made of steel, silver and brass; it was finely decorated and looked like a renaissance table clock. His dedication to the emperor engraved on the height of the automobile also reads "..to brand easy to ignorant people, add-on, subtraction, multiplication and even division".^[48]
• In 1730, the French Academy of Sciences certified iii machines designed past Hillerin de Boistissandeau. The kickoff one used a single-tooth carry mechanism which, according to Boistissandeau, wouldn't work properly if a carry had to be moved more than two places; the two other machines used springs that were gradually armed until they released their free energy when a carry had to be moved forward. It was similar to Pascal's calculator but instead of using the free energy of gravity Boistissandeau used the energy stored into the springs.^[49]
• In 1770, Philipp Matthäus Hahn, a High german pastor, built ii circular computing machines based on Leibniz' cylinders.^{[50] [51]} J. C. Schuster, Hahn's blood brother in constabulary, congenital a few machines of Hahn's pattern into the early 19th century.^[52]
• In 1775, Lord Stanhope of the Britain designed a pinwheel machine. It was ready in a rectangular box with a handle on the side. He also designed a machine using Leibniz wheels in 1777.^[53] "In 1777 Stanhope produced the Logic Demonstrator, a car designed to solve problems in formal logic. This device marked the beginning of a new approach to the solution of logical problems by mechanical methods."^[xl]
• In 1784, Johann-Helfrich Müller congenital a auto very similar to Hahn'southward machine.^[54]

The 19th century [edit]

Overview [edit]

Luigi Torchi invented the first directly multiplication machine in 1834.^[55] This was also the second key-driven auto in the world, following that of James White (1822).^[56]

The mechanical reckoner industry started in 1851 Thomas de Colmar released his simplified Arithmomètre, which was the first automobile that could be used daily in an function environment.

For xl years,^[57] the arithmometer was the merely mechanical calculator available for sale and was sold all over the world. By 1890, about ii,500 arithmometers had been sold^[58] plus a few hundreds more from ii licensed arithmometer clone makers (Burkhardt, Germany, 1878 and Layton, United kingdom of great britain and northern ireland, 1883). Felt and Tarrant, the only other competitor in true commercial production, had sold 100 comptometers in three years.^[59]

The 19th century too saw the designs of Charles Babbage calculating machines, kickoff with his difference engine, started in 1822, which was the beginning automatic calculator since it continuously used the results of the previous operation for the next 1, and 2nd with his analytical engine, which was the showtime programmable reckoner, using Jacquard's cards to read program and data, that he started in 1834, and which gave the blueprint of the mainframe computers congenital in the middle of the 20th century.^[threescore]

Desktop Mechanical Calculators in product during the 19th century

Desktop calculators produced [edit]

Front panel of a Thomas Arithmometer with its movable result carriage extended

• In 1851, Thomas de Colmar simplified his arithmometer past removing the one-digit multiplier/divider. This fabricated it a elementary calculation auto, but thanks to its moving carriage used equally an indexed accumulator, it still immune for like shooting fish in a barrel multiplication and division under operator control. The arithmometer was now adapted to the manufacturing capabilities of the time; Thomas could therefore industry consistently a sturdy and reliable machine.^[61] Manuals were printed and each machine was given a serial number. Its commercialization launched the mechanical calculator industry.^[62] Banks, insurance companies, government offices started to use the arithmometer in their twenty-four hour period-to-day operations, slowly bringing mechanical desktop calculators into the function.
• In 1878 Burkhardt, of Frg, was the commencement to manufacture a clone of Thomas' arithmometer. Until then Thomas de Colmar had been the simply manufacturer of desktop mechanical calculators in the globe and he had manufactured well-nigh 1,500 machines.^[63] Eventually twenty European companies will manufacture clones of Thomas' arithmometer until WWII.
• Dorr East. Felt, in the U.S., patented the Comptometer in 1886. It was the starting time successful key-driven adding and computing car. ["Key-driven" refers to the fact that just pressing the keys causes the event to exist calculated, no separate lever or crank has to be operated. Other machines are sometimes chosen "cardinal-set up".] In 1887, he joined with Robert Tarrant to form the Felt & Tarrant Manufacturing Company.^[64] The comptometer-type calculator was the first machine to receive an all-electronic calculator engine in 1961 (the ANITA marking VII released by Sumlock comptometer of the UK).
• In 1890 W. T. Odhner got the rights to manufacture his calculator back from Königsberger & C, which had held them since it was first patented in 1878, but had not really produced anything. Odhner used his Saint Petersburg workshop to manufacture his calculator and he built and sold 500 machines in 1890. This manufacturing operation shut down definitively in 1918 with 23,000 machines produced. The Odhner Arithmometer was a redesigned version of the Arithmometer of Thomas de Colmar with a pinwheel engine, which made it cheaper to industry and gave it a smaller footprint while keeping the advantage of having the aforementioned user interface.^[65]
• In 1892 Odhner sold the Berlin branch of his factory, which he had opened a twelvemonth earlier, to Grimme, Natalis & Co. They moved the manufactory to Braunschweig and sold their machines under the brand name of Brunsviga (Brunsviga is the Latin name of the boondocks of Braunschweig).^[66] This was the first of many companies which would sell and manufacture clones of Odhner'due south machine all over the world; somewhen millions were sold well into the 1970s.^[65]
• In 1892, William S. Burroughs began commercial manufacture of his press adding calculator^[67] Burroughs Corporation became one of the leading companies in the accounting machine and figurer businesses.
• The "Millionaire" estimator was introduced in 1893. Information technology immune direct multiplication past any digit – "one plough of the crank for each figure in the multiplier". It independent a mechanical product lookup tabular array, providing units and tens digits by differing lengths of posts.^[68] Another direct multiplier was part of the Moon-Hopkins billing machine; that company was acquired by Burroughs in the early 20th century.

19th century Comptometer in a wooden example

Automatic mechanical calculators [edit]

The London Science Museum'due south working departure engine, built a century and a one-half after Charles Babbage's design.

• In 1822, Charles Babbage presented a pocket-sized cogwheel assembly that demonstrated the operation of his difference engine,^[69] a mechanical reckoner which would be capable of holding and manipulating seven numbers of 31 decimal digits each. It was the first fourth dimension that a computing machine could piece of work automatically using as input results from its previous operations.^[60] It was the first calculating machine to utilize a printer. The development of this machine, afterward chosen "Difference Engine No. i," stopped effectually 1834.^[lxx]
• In 1847, Babbage began piece of work on an improved difference engine design—his "Difference Engine No. 2." None of these designs were completely built by Babbage. In 1991 the London Science Museum followed Babbage'due south plans to build a working Deviation Engine No. 2 using the technology and materials available in the 19th century.
• In 1855, Per Georg Scheutz completed a working deviation engine based on Babbage's design. The automobile was the size of a piano, and was demonstrated at the Exposition Universelle in Paris in 1855. It was used to create tables of logarithms.
• In 1875, Martin Wiberg re-designed the Babbage/Scheutz deviation engine and congenital a version that was the size of a sewing machine.

Programmable mechanical calculators [edit]

Minimal merely working demonstration office of the factory from the Analytical engine, finished by Babbage's son effectually 1906

• In 1834, Babbage started to design his belittling engine, which will become the undisputed antecedent of the modern mainframe computer^[71] with two divide input streams for data and plan (a primitive Harvard architecture), printers for outputting results (three different kind), processing unit (mill), memory (shop) and the kickoff-e'er set of programming instructions. In the proposal that Howard Aiken gave IBM in 1937 while requesting funding for the Harvard Mark I which became IBM'due south entry machine in the computer industry, we tin read: "Few calculating machines have been designed strictly for application to scientific investigations, the notable exceptions beingness those of Charles Babbage and others who followed him. In 1812 Babbage conceived the idea of a calculating machine of a college type than those previously synthetic to be used for calculating and press tables of mathematical functions. ....After abandoning the difference engine, Babbage devoted his energy to the design and construction of an belittling engine of far higher powers than the difference engine..."^[72]
• In 1843, during the translation of a French article on the analytical engine, Ada Lovelace wrote, in ane of the many notes she included, an algorithm to compute the Bernoulli numbers. This is considered the first figurer program.
• From 1872 until 1910, Henry Babbage worked intermittently on creating the mill, the "central processing unit" of his father's car. Subsequently a few setbacks, he gave in 1906 a successful demonstration of the manufactory which printed the outset 44 multiples of pi with 29 places of figures.

Greenbacks registers [edit]

The greenbacks register, invented by the American saloonkeeper James Ritty in 1879, addressed the erstwhile bug of disorganization and dishonesty in business transactions.^[73] It was a pure adding machine coupled with a printer, a bell and a ii-sided display that showed the paying party and the store owner, if he wanted to, the amount of money exchanged for the current transaction.

The cash register was easy to use and, unlike genuine mechanical calculators, was needed and chop-chop adopted by a great number of businesses. "Eighty iv companies sold cash registers between 1888 and 1895, merely three survived for any length of fourth dimension".^[74]

In 1890, six years later John Patterson started NCR Corporation, twenty,000 machines had been sold past his company alone against a total of roughly three,500 for all genuine calculators combined.^[75]

By 1900, NCR had built 200,000 cash registers^[76] and there were more than companies manufacturing them, compared to the "Thomas/Payen" arithmometer company that had just sold effectually 3,300^[77] and Burroughs had simply sold one,400 machines.^[78]

Prototypes and limited runs [edit]

The arithmometers built from 1820 to 1851 had a one-digit multiplier/divider cursor (ivory top) is on the left. But prototypes of these machines were built.

• In 1820, Thomas de Colmar patented the Arithmometer. Information technology was a true 4 performance machine with a one digit multiplier/divider (The Millionaire estimator released 70 years subsequently had a similar user interface^[79]). He spent the next xxx years and 300,000 Francs developing his car.^[80] This design was replaced in 1851 by the simplified arithmometer which was but an adding motorcar.
• From 1840, Didier Roth patented and built a few computing machines, one of which was a directly descendant of Pascal's computer.
• In 1842, Timoleon Maurel invented the Arithmaurel, based on the Arithmometer, which could multiply ii numbers by merely entering their values into the machine.
• In 1845, Izrael Abraham Staffel showtime exhibited a machine that was able to add, decrease, divide, multiply and obtain a square root.
• Around 1854, Andre-Michel Guerry invented the Ordonnateur Statistique, a cylindrical device designed to aid in summarizing the relations among data on moral variables (crime, suicide, etc.)^[81]
• In 1872, Frank S. Baldwin in the U.Due south. invented a pinwheel computer.
• In 1877 George B. Grant of Boston, MA, began producing the Grant mechanical calculating car capable of addition, subtraction, multiplication and partition.^[82] The auto measured 13x5x7 inches and contained eighty working pieces made of contumely and tempered steel. Information technology was commencement introduced to the public at the 1876 Centennial Exposition in Philadelphia.^[83]
• In 1883, Edmondson of the UK patented a circular stepped drum machine^[84]

Detail of an early calculating auto invented by Didier Roth around 1840. This motorcar is a direct descendant of Pascal's Computer.

1900s to 1970s [edit]

Mechanical calculators achieve their zenith [edit]

Mechanical calculator from 1914

An Addiator tin can be used for addition and subtraction.

Two dissimilar classes of mechanisms had go established by this time, reciprocating and rotary. The former type of mechanism was operated typically past a limited-travel hand crank; some internal detailed operations took place on the pull, and others on the release part of a consummate cycle. The illustrated 1914 machine is this type; the crank is vertical, on its right side. Later on, some of these mechanisms were operated by electric motors and reduction gearing that operated a crank and connecting rod to catechumen rotary motion to reciprocating.

The latter type, rotary, had at least one main shaft that made one [or more than] continuous revolution[s], one addition or subtraction per plow. Numerous designs, notably European calculators, had handcranks, and locks to ensure that the cranks were returned to exact positions once a turn was complete.

The kickoff half of the 20th century saw the gradual development of the mechanical calculator mechanism.

The Dalton adding-listing machine introduced in 1902 was the showtime of its type to utilize only ten keys, and became the first of many different models of "10-key add-listers" manufactured past many companies.

In 1948 the cylindrical Curta computer, which was compact enough to be held in one manus, was introduced afterward being adult by Brusk Herzstark in 1938. This was an farthermost development of the stepped-gear calculating mechanism. Information technology subtracted by adding complements; between the teeth for addition were teeth for subtraction.

From the early on 1900s through the 1960s, mechanical calculators dominated the desktop computing market place. Major suppliers in the Usa included Friden, Monroe, and SCM/Marchant. These devices were motor-driven, and had movable carriages where results of calculations were displayed by dials. Most all keyboards were full – each digit that could be entered had its ain cavalcade of nine keys, 1..9, plus a column-clear fundamental, permitting entry of several digits at one time. (See the illustration beneath of a Marchant Figurematic.) One could call this parallel entry, by way of contrast with x-cardinal series entry that was commonplace in mechanical calculation machines, and is now universal in electronic calculators. (Nearly all Friden calculators, too as some rotary (German) Diehls had a 10-key auxiliary keyboard for entering the multiplier when doing multiplication.) Full keyboards more often than not had ten columns, although some lower-cost machines had viii. About machines made by the three companies mentioned did not print their results, although other companies, such as Olivetti, did make printing calculators.

In these machines, addition and subtraction were performed in a single performance, every bit on a conventional adding automobile, just multiplication and sectionalization were accomplished past repeated mechanical additions and subtractions. Friden made a calculator that also provided foursquare roots, basically by doing division, but with added machinery that automatically incremented the number in the keyboard in a systematic fashion. The last of the mechanical calculators were probable to take brusque-cut multiplication, and some x-primal, serial-entry types had decimal-point keys. However, decimal-point keys required significant internal added complexity, and were offered only in the last designs to be made. Handheld mechanical calculators such as the 1948 Curta continued to be used until they were displaced past electronic calculators in the 1970s.

	Walther WSR160 (one of the most common calculators in central Europe) (1960)
Mechanism of mechanical calculator

Typical European iv-performance machines use the Odhner machinery, or variations of it. This kind of machine included the Original Odhner, Brunsviga and several following imitators, starting from Triumphator, Thales, Walther, Facit up to Toshiba. Although most of these were operated by handcranks, at that place were motor-driven versions. Hamann calculators externally resembled pinwheel machines, but the setting lever positioned a cam that disengaged a drive pawl when the punch had moved far enough.

Although Dalton introduced in 1902 start 10-key printing calculation (two operations, the other existence subtraction) motorcar, these features were non present in computing (four operations) machines for many decades. Facit-T (1932) was the starting time 10-central computing automobile sold in large numbers. Olivetti Divisumma-14 (1948) was the showtime calculating machine with both printer and a x-key keyboard.

Full-keyboard machines, including motor-driven ones, were also built until the 1960s. Among the major manufacturers were Mercedes-Euklid, Archimedes, and MADAS in Europe; in the USA, Friden, Marchant, and Monroe were the principal makers of rotary calculators with carriages. Reciprocating calculators (most of which were calculation machines, many with integral printers) were made by Remington Rand and Burroughs, among others. All of these were key-set. Felt & Tarrant fabricated Comptometers, as well every bit Victor, which were cardinal-driven.

The bones machinery of the Friden and Monroe was a modified Leibniz cycle (meliorate known, peradventure informally, in the USA as a "stepped drum" or "stepped reckoner"). The Friden had an unproblematic reversing drive between the body of the machine and the accumulator dials, and so its chief shaft always rotated in the aforementioned management. The Swiss MADAS was similar. The Monroe, withal, reversed direction of its main shaft to decrease.

The earliest Marchants were pinwheel machines, but near of them were remarkably sophisticated rotary types. They ran at one,300 addition cycles per minute if the [+] bar is held downwardly. Others were limited to 600 cycles per minute, because their accumulator dials started and stopped for every bicycle; Marchant dials moved at a steady and proportional speed for continuing cycles. Almost Marchants had a row of nine keys on the extreme right, every bit shown in the photo of the Figurematic. These simply made the machine add for the number of cycles respective to the number on the primal, and and so shifted the carriage one place. Even nine add cycles took only a short time.

In a Marchant, nearly the beginning of a cycle, the accumulator dials moved downward "into the dip", away from the openings in the cover. They engaged drive gears in the body of the machine, which rotated them at speeds proportional to the digit being fed to them, with added motion (reduced 10:1) from carries created past dials to their right. At the completion of the bike, the dials would be misaligned like the pointers in a traditional watt-hour meter. However, as they came up out of the dip, a constant-atomic number 82 disc cam realigned them by style of a (limited-travel) spur-gear differential. Likewise, carries for lower orders were added in past another, planetary differential. (The machine shown has 39 differentials in its [20-digit] accumulator!)

In whatever mechanical computer, in issue, a gear, sector, or some like device moves the accumulator past the number of gear teeth that corresponds to the digit existence added or subtracted – iii teeth changes the position by a count of three. The great majority of basic calculator mechanisms move the accumulator by starting, then moving at a abiding speed, and stopping. In particular, stopping is disquisitional, because to obtain fast performance, the accumulator needs to move chop-chop. Variants of Geneva drives typically block overshoot (which, of form, would create incorrect results).

However, 2 different basic mechanisms, the Mercedes-Euklid and the Marchant, move the dials at speeds corresponding to the digit existence added or subtracted; a [1] moves the accumulator the slowest, and a [nine], the fastest. In the Mercedes-Euklid, a long slotted lever, pivoted at one finish, moves nine racks ("straight gears") endwise by distances proportional to their distance from the lever's pivot. Each rack has a drive pivot that is moved by the slot. The rack for [1] is closest to the pivot, of course. For each keyboard digit, a sliding selector gear, much similar that in the Leibniz wheel, engages the rack that corresponds to the digit entered. Of class, the accumulator changes either on the forward or reverse stroke, but not both. This mechanism is notably unproblematic and relatively like shooting fish in a barrel to manufacture.

The Marchant, notwithstanding, has, for every ane of its ten columns of keys, a nine-ratio "preselector transmission" with its output spur gear at the top of the machine'due south body; that gear engages the accumulator gearing. When one tries to work out the numbers of teeth in such a manual, a straightforward approach leads one to consider a mechanism like that in mechanical gasoline pump registers, used to indicate the total price. However, this mechanism is seriously bulky, and utterly impractical for a reckoner; xc-tooth gears are likely to be found in the gas pump. Practical gears in the computing parts of a calculator cannot have xc teeth. They would be either besides big, or too frail.

Given that nine ratios per column implies significant complexity, a Marchant contains a few hundred private gears in all, many in its accumulator. Basically, the accumulator dial has to rotate 36 degrees (1/10 of a plow) for a [one], and 324 degrees (9/ten of a plough) for a [9], not assuasive for incoming carries. At some point in the gearing, one tooth needs to pass for a [ane], and nine teeth for a [9]. In that location is no way to develop the needed movement from a driveshaft that rotates one revolution per cycle with few gears having practical (relatively small) numbers of teeth.

The Marchant, therefore, has three driveshafts to feed the little transmissions. For one cycle, they rotate 1/2, one/4, and 1/12 of a revolution. [1]. The i/2-plough shaft carries (for each column) gears with 12, xiv, sixteen, and 18 teeth, corresponding to digits half dozen, seven, viii, and 9. The 1/four-turn shaft carries (also, each column) gears with 12, sixteen, and twenty teeth, for 3, 4, and 5. Digits [1] and [ii] are handled past 12 and 24-tooth gears on the i/12-revolution shaft. Practical pattern places the twelfth-rev. shaft more afar, and so the 1/4-turn shaft carries freely-rotating 24 and 12-tooth idler gears. For subtraction, the driveshafts reversed direction.

In the early on part of the cycle, one of five pendants moves off-center to engage the advisable bulldoze gear for the selected digit.

Some machines had as many every bit 20 columns in their full keyboards. The monster in this field was the Duodecillion made past Burroughs for exhibit purposes.

For sterling currency, £/southward/d (and even farthings), there were variations of the bones mechanisms, in detail with different numbers of gear teeth and accumulator dial positions. To accommodate shillings and pence, extra columns were added for the tens digit[s], x and 20 for shillings, and 10 for pence. Of course, these functioned as radix-20 and radix-12 mechanisms.

A variant of the Marchant, called the Binary-Octal Marchant, was a radix-8 (octal) motorcar. It was sold to check very early on vacuum-tube (valve) binary computers for accuracy. (Back then, the mechanical computer was much more reliable than a tube/valve figurer.)

Too, there was a twin Marchant, comprising two pinwheel Marchants with a mutual drive crank and reversing gearbox.^[85] Twin machines were relatively rare, and apparently were used for surveying calculations. At least one triple machine was made.

The Facit calculator, and 1 similar to it, are basically pinwheel machines, but the array of pinwheels moves sidewise, instead of the carriage. The pinwheels are biquinary; digits ane through 4 cause the corresponding number of sliding pins to extend from the surface; digits 5 through nine also extend a five-tooth sector likewise as the aforementioned pins for 6 through 9.

The keys operate cams that operate a swinging lever to offset unlock the pivot-positioning cam that is part of the pinwheel mechanism; further movement of the lever (by an amount determined past the key'south cam) rotates the pivot-positioning cam to extend the necessary number of pins.^[86]

Stylus-operated adders with circular slots for the stylus, and side-past -side wheels, as made past Sterling Plastics (USA), had an ingenious anti-overshoot machinery to ensure accurate carries.

		Marchant Figurematic (1950–52)
		Odhner Arithmometer (1890–1970s)

The end of an era [edit]

Mechanical calculators connected to be sold, though in rapidly decreasing numbers, into the early on 1970s, with many of the manufacturers endmost downward or existence taken over. Comptometer type calculators were frequently retained for much longer to be used for adding and listing duties, especially in accounting, since a trained and skilled operator could enter all the digits of a number in i movement of the easily on a comptometer quicker than was possible serially with a 10-primal electronic computer. In fact, it was quicker to enter larger digits in two strokes using only the lower-numbered keys; for instance, a ix would be entered as 4 followed by 5. Some key-driven calculators had keys for every column, just only one through v; they were correspondingly compact. The spread of the computer rather than the simple electronic calculator put an cease to the comptometer. Also, past the end of the 1970s, the slide rule had become obsolete.

See also [edit]

• Abacus
• Adding car
• Calculator
• History of computing hardware
• Mechanical computer
• Tabulating auto
• George Dark-brown (inventor)

References [edit]

1. ^ Michael Williams, History of Computing Technology, IEEE Calculator Society, p. 122 (1997)
2. ^ Michael Williams, History of Computing Engineering science, IEEE Estimator Society, p. 124, 128 (1997)
3. ^ Prof. René Cassin, Pascal tercentenary celebration, London, (1942), Mag Nature
4. ^ ^{a b} Jean Marguin (1994), p. 48
5. ^ See Pascal'due south calculator#Competing designs
6. ^ Abreast two arithmometer clone makers from Federal republic of germany and England, the but other company to offering calculators for sale was Felt & Tarrant from the USA which started selling their comptometer in 1887 just had only sold 100 machines by 1890.
7. ^ Ernst Martin p. 133 (1925)
8. ^ Ernst Martin p. 23 (1925)
9. ^ #MARG,Jean Marguin p. 171, (1994)
10. ^ Anthony Hyman, Charles Babbage, pioneer of the computer, 1982
11. ^ "The introduction of punched cards into the new engine was important not only as a more user-friendly form of control than the drums, or because programs could now be of unlimited extent, and could be stored and repeated without the danger of introducing errors in setting the machine by hand; information technology was of import likewise because information technology served to crystallize Babbage's feeling that he had invented something really new, something much more than than a sophisticated computing machine." Bruce Collier, 1970
12. ^ I. Bernard Cohen, p. 66-67, (2000)
13. ^ Brian Randell, p. 187, 1975
14. ^ Please see Pascaline#Pascal versus Schickard
15. ^ "The arithmetical car produces effects which approach nearer to thought than all the deportment of animals. But it does cypher which would enable us to attribute will to it, as to the animals.", Pascal, Pensées Bartleby.com, Dandy Books online, Blaise Pasdcal, Thoughts
16. ^ ^{a b} Magazine Nature, (1942)
17. ^ Scripta Mathematica, p. 128 (1932)
18. ^ From the calculating machine of Pascal to the computer, p. 43 (1990)
19. ^ (fr) La Machine d'arithmétique, Blaise Pascal, Wikisource
20. ^ Guy Mourlevat, p. 12 (1988)
21. ^ Courrier du CIBP, N°8, p. 9, (1986)
22. ^ "...et si blocage il y avait, la machine était pratiquement inutilisable, ce qui ne fut jamais signalé dans les textes du XVIIIe siecle parmi ses défaults" Guy Mourlevat, p. 30 (1988)
23. ^ ^{a b} Jean Marguin, p. 64-65 (1994)
24. ^ Scripta Mathematica, p. 149 (1932)
25. ^ Morar, Florin-Stefan (March 2015). "Reinventing machines: the manual history of the Leibniz estimator". The British Journal for the History of Science. 48 (1): 123–146. doi:10.1017/S0007087414000429. ISSN 0007-0874. PMID 25833800. S2CID 38193192.
26. ^ David Smith, p. 173-181 (1929)
27. ^ Equally quoted in Smith 1929, pp. 180–181 harvnb error: no target: CITEREFSmith1929 (help)
28. ^ Meet http://things-that-count.net
29. ^ Translated from "j'en composai une troisième qui va par ressorts et qui est très simple en sa structure. C'est celle de laquelle, comme j'ai déjà dit, je me suis servi plusieurs fois, au vu et su d'une infinité de personnes, et qui est encore en état de servir autant que jamais. Toutefois, en la perfectionnant toujours, je trouvai des raisons de la changer" Avis nécessaire à ceux qui auront curiosité de voir la Machine d'Arithmétique et de southward'en servir Wikisource: La Auto d'arithmétique, Blaise Pascal
30. ^ Quoted in David Smith, p. 173, (1929)
31. ^ Michael Williams, p. 124, 128 (1997) for Schikard's machine and the fact that the machines built past Burattini, Morland and Grillet were calculating clocks without a completely effective comport mechanism.
32. ^ History of calculator (retrieved on 1 February 2012)
33. ^ Michael Williams, p. 122 (1997)
34. ^ Michael Williams, p. 124, 128 (1997)
35. ^ "The appearance of this modest avorton disturbed me to the utmost and information technology dampened the enthusiasm with which I was developing my calculator and so much that I immediately allow go all of my employees..." translated from the French: "L'aspect de ce petit avorton me déplut au dernier bespeak et refroidit tellement l'ardeur avec laquelle je faisais lors travailler à l'accomplissement de mon modèle qu'à l'instant même je donnai congé à tous les ouvriers..."
36. ^ "But, afterward, Lord Chancellor of France [...] granted me a royal privilege which is non usual, and which will suffocate before their birth all these illegitimate avortons which, past the style, could merely be born of the legitimate and necessary alliance of theory and art." translated from the French: "Mais, quelque temps après, Monseigneur le Chancelier [...] par la grâce qu'il me fit de g'accorder un privilège qui n'est pas ordinaire, et qui étouffe avant leur naissance tous ces avortons illégitimes qui pourraient être engendrés d'ailleurs que de la légitime et nécessaire alliance de la théorie avec fifty'art"
37. ^ "...a useless piece, perfectly clean, polished and well filed on the outside but so imperfect within that information technology is of no use whatsoever." translated from the French: "...qu'une pièce inutile, propre véritablement, polie et très bien limée par le dehors, mais tellement imparfaite au dedans qu'elle n'est d'aucun usage"
38. ^ All the quotes in this paragraph are found in (fr) Wikisource: Avis nécessaire à ceux qui auront curiosité de voir la Machine d'Arithmétique et de southward'en servir.
39. ^ Picture of Burattini's machine Archived 9 June 2010 at the Wayback Motorcar Florence, Istituto e Museo di Storia della Scienza, inv. 3179 (accessed on January, 09 2012)
40. ^ ^{a b} A reckoner Chronicle, 300 years of counting and reckoning tools, p. 12, IBM
41. ^ Michael Williams, p.140 (1997)
42. ^ Picture of Morland multiplying motorcar Florence, Istituto eastward Museo di Storia della Scienza, inv. 679 (retrieved on January, 09 2012)
43. ^ They belong to the Musée des Arts et Métiers in Paris.
44. ^ "Grillet's machine doesn't fifty-fifty deserve the name of machine" translated from the French "La auto de Grillet ne mérite donc pas même le nom de machine", Jean Marguin, p.76 (1994)
45. ^ Copy of Poleni's automobile (it) Museo Nazionale della Scienza e della Tecnologia Leonardo Da Vinci. Retrieved 4 Oct 2010
46. ^ Jean Marguin, p. 93-94 (1994)
47. ^ translated from the French: "De plus le report ne s'effectuant pas en pour, la machine devait se bloquer au-delà de quelques reports simultanés", Jean Marguin, p.78 (1994)
48. ^ Jean Marguin, p.94-96 (1994)
49. ^ #MARG, Jean Marguin, pages lxxx–81 (1994)
50. ^ Marguin, p.83 (1994)
51. ^ Motion-picture show of Hahn's Figurer IBM Drove of mechanical calculators
52. ^ Jean Marguin, pages 84–86 (1994)
53. ^ Door E. Felt, p.xv-16 (1916)
54. ^ "CNUM – 8KU54-ii.v : p.249 – im.253". cnum.cnam.fr.
55. ^ "History of Computers and Computing, Mechanical calculators, 19th century, Luiggi Torchi". history-figurer.com.
56. ^ Roegel, Denis (2016). "Before Torchi and Schwilgué, There Was White". IEEE Register of the History of Computing. 38 (4): 92–93. doi:10.1109/MAHC.2016.46.
57. ^ This is i third of the 120 years that this industry lasted
58. ^ "world wide web.arithmometre.org". arithmometre.org.
59. ^ Felt, Dorr E. (1916). Mechanical arithmetic, or The history of the counting car. Chicago: Washington Institute. p. 4.
60. ^ ^{a b} "The calculating engines of English mathematician Charles Babbage (1791–1871) are among the most celebrated icons in the prehistory of computing. Babbage's Difference Engine No.one was the start successful automated figurer and remains one of the finest examples of precision engineering of the time. Babbage is sometimes referred to as "father of computing." The International Charles Babbage Social club (later the Charles Babbage Institute) took his proper name to honor his intellectual contributions and their relation to modern computers." Charles Babbage Institute (folio. Retrieved 1 February 2012).
61. ^ Ifrah Thousand., The Universal History of Numbers, vol three, page 127, The Harvill Printing, 2000
62. ^ Chase M.C.: History of Mechanical Computing Machinery, Vol. 2, Number 3, July 1980, IEEE Annals of the History of Computing, p. 204
63. ^ Serial numbers and Years of manufacturing www.arithmometre.org, Valéry Monnier
64. ^ J.A.5. Turck, Origin of modern calculating machines, The Western Gild of Engineers, 1921, p. 75
65. ^ ^{a b} G. Trogemann, pages: 39–45
66. ^ David J. Shaw: The Cathedral Libraries Catalogue, The British Library and the Bibliographical Guild, 1998
67. ^ J.A.V. Turck, Origin of modern computing machines, The Western Society of Engineers, 1921, p. 143
68. ^ Wolff, John (30 May 2007). "The "Millionaire" Computing Auto - Technical Clarification". John Wolff's Spider web Museum . Retrieved 30 December 2019.
69. ^ James Essinger, p.76 (2004)
70. ^ "The better part of my alive has now been spent on that auto, and no progress whatever having been made since 1834...", Charles Babbage, quoted in Irascible Genius, 1964, p.145
71. ^ "It is reasonable to inquire, therefore, whether it is possible to devise a automobile which will practice for mathematical computation what the automatic lathe has done for applied science. The first suggestion that such a automobile could be made came more than a hundred years ago from the mathematician Charles Babbage. Babbage's ideas take merely been properly appreciated in the last ten years, but we now realize that he understood clearly all the fundamental principles which are embodied in modern digital computers" B. V. Bowden, 1953, pp. half dozen,7
72. ^ Howard Aiken, 1937, reprinted in The origins of Digital computers, Selected Papers, Edited by Brian Randell, 1973
73. ^ NCR Retrospective website. Retrieved October, 02 2012
74. ^ History of the cash register. Retrieved October, 05 2012
75. ^ See the number of machines built in 1890 in this paragraph
76. ^ Dick and Joan'southward antique. Retrieved October, 02 2012
77. ^ List of series numbers by dates arithmometre.org. Retrieved x October 2012
78. ^ Before the computer, James Due west. Cortada, p.34 ISBN 0-691-04807-10
79. ^ A notable divergence was that the Millionaire computer used an internal mechanical production lookup table versus a repeated addition or subtraction until a counter was decreased down to nada and stopped the machine for the arithmometer
80. ^ Fifty'ami des Sciences 1856, p. 301 www.arithmometre.org (page. Retrieved 22 September 2010)
81. ^ Larousse, P. (1886), Thou dictionnaire universel du XIX siècle, Paris, entry for A-K Guerry
82. ^ Hook & Norman p.252 (2001): "Grant adult two models of his calculating automobile: a Barrel model, which he exhibited at the Centennial Exposition along with his deviation engine; and a Rack and Pinion model, of which he was able to sell 125 examples. Although Grant never made much coin from his calculating machines, his experiences in designing and amalgam them led him to constitute the highly successful Grant Gear Works, which helped to pioneer the gear-cutting industry in the United states."
83. ^ "Improved Calculating Machine", "Scientific American" Vol. XXXVI, No. 19, 12 May 1877 p.294 New York: Munn &Visitor (Publisher)
84. ^ Patent application in French from www.ami19.org scanned past Valéry Monnier (retrieved on 12 Jan 2012)
85. ^ "The Twin Marchant".
86. ^ "John Wolff'south Web Museum - Facit C1-13 - Technical Description".

Sources [edit]

• De la machine à calculer de Pascal à 50'ordinateur (in French). Paris, France: Musée National des Techniques, CNAM. 1990. ISBNii-908207-07-9.
• Trogemann, G.; Nitussov, A. (2001). Computing in Russia. Federal republic of germany: GWV-Vieweg. ISBN3-528-05757-2.
• Felt, Dorr Due east. (1916). Mechanical arithmetics, or The history of the counting motorcar. Chicago: Washington Establish.
• Marguin, Jean (1994). Histoire des instruments et machines à calculer, trois siècles de mécanique pensante 1642–1942 (in French). Hermann. ISBN978-2-7056-6166-3.
• Mourlevat, Guy (1988). Les machines arithmétiques de Blaise Pascal (in French). Clermont-Ferrand: La Française d'Edition et d'Imprimerie.
• Taton, René (1969). Histoire du calcul. Que sais-je ? n° 198 (in French). Presses universitaires de France.
• Turck, J.A.V. (1921). Origin of Modern Calculating Machines. The Western Society of Engineers. Reprinted by Arno Press, 1972 ISBN 0-405-04730-4.
• Ginsburg, Jekuthiel (2003). Scripta Mathematica (Septembre 1932-Juin 1933). Kessinger Publishing, LLC. ISBN978-0-7661-3835-3.
• Martin, Ernst (1992) [1925]. The Charles Babbage Found (ed.). The Calculating Machines (Die Rechenmaschinen). Cambridge, Massachusetts: The MIT Press.
• Cohen, I. Bernard (2000). Howard Aiken : Portrait of a Computer Pioneer. Cambridge, Massachusetts: The MIT Press. ISBNix-780262-531795.
• Smith, David Eugene (1929). A Source Book in Mathematics . New York and London: McGraw-Hill Volume Company, Inc.
• Moseley, Maboth (1964). Irascible Genius, Charles Babbage Inventor. London: Hutchinson & Co, Ltd.
• Bowden, B. V. (1953). Faster than idea. New York, Toronto, London: Pitman publishing corporation.
• Williams, Michael R. (1997). History of Calculating Technology. Los Alamitos, California: IEEE Computer Social club. ISBN0-8186-7739-two.
• Randell, Brian (1973). The origins of Digital computers, Selected Papers. Springer-Verlag. ISBN3-540-06169-X.
• IBM. A calculator Chronicle, 300 years of counting and reckoning tools . New York.
• Collier, Bruce (1990). The little engine that could've: The calculating machines of Charles Babbage. Garland Publishing Inc. ISBN0-8240-0043-9.
• Essinger, James (2004). Jacquard's Web . Oxford University Printing. ISBN0-xix-280577-0.
• Hook, Diana H.; Norman, Jeremy Grand. (2001). Origins of Internet. Novato, California: historyofscience.com. ISBN0-930405-85-4.
• M.E.P (31 October 1942). "Pascal tercentenary celebration". Nature. London. 150 (3809): 527. Bibcode:1942Natur.150..527M. doi:ten.1038/150527a0.
• Prof. Southward. Chapman (31 Oct 1942). "Blaise Pascal (1623-1662) Tercentenary of the calculating machine". Nature. London. 150: 508–509. Bibcode:1942Natur.150..508C. doi:10.1038/150508a0.
• "Usage de la machine". Courrier du Centre International Blaise Pascal (in French). Clermont-Ferrand (eight): four–25. 1986.

External links [edit]

• Wolff, John (2014). "Computing Machines". John Wolff'south Web Museum.
• Mařík, Robert Mechanical Calculators playlist on YouTube
• Media related to Mechanical calculators at Wikimedia Commons

searsthistrair.blogspot.com

Source: https://en.wikipedia.org/wiki/Mechanical_calculator

Share this post